
      function addUpTo(n: number){
          let total = 0;
  
          for (let i = 0; i < n; i++) {
              total =+ i;
          }
      
          return total;
      }

Big O Notation

Big O Notation is a formal way (or rather a mathematical way) to measure the execution behavior of an algorithm. Usually used to measure the relations between the size of input (n) and the runtime execution of a function f(n).

We say that and algorithm is O(f(n)) if the number of operations that the computer has to do is less than a constant times f(n).

Quite gibberish but that definition means that a function or an algorithm could be:

1. Constant — O(1)

No matter how small or huge the input is, the output will stay constant. This is because the operations are independent and not affected by the input (n). If the number of operations are 3, then no matter the input whether it is 100, 1000, 100K, 1M, or even 1B, the output will always constant to 3.

2. Logarithmic — O(log n)

Logarithm is a opposite operation of exponentiation. So O(log n) refers to a function (or algorithm, or step in an algorithm) working in an amount of time proportional to the logarithm of the size of the input. This type of Big O commonly used in a divide-and-conquer algorithm like binary search. ^{Read More}

3. Linear — O(n)

Linear means a function with the input of (n) scales with the input, if the input grows larger, the output (execution time) grows as well.

4. Linearithmic — O(n log n)

Linearithmic time (O(n log n)) is the Muddy Mudskipper of time complexities—the worst of the best (although, less grizzled and duplicitous). It is a moderate complexity that floats around linear time (O(n)) until input reaches advanced size. It is slower than logarithmic time, but faster than the less favorable, less performant time complexities. ^{Read More}

5. Quadratic — O(n²)

Quadratic means that a function with the input of n squared related to the square of the input (n). If the input is 5, then the output is 5² = 25.

6. Exponential — O(2ⁿ)

The algorithm or a function with exponential characteristics will growth exponentiatially with the growth of n. The complexity starts very small, then rising exponentially until the last of the input.

7. Factorial — O(n!)

This is worst of the worst, and should be avoided. Remember when doing factorial in high school, 5! (5 factorial) is equal to 5 * 4 * 3 * 2 * 1 = 120.

8. Or could be something entirely different formula!

Big O Complexity Chart

Here is the cheating-chart to compare between each complexity.

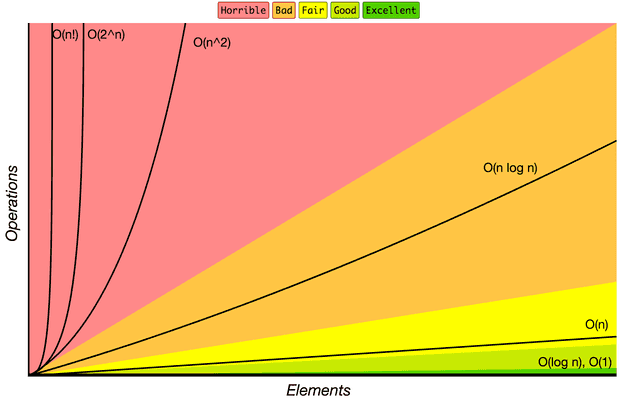
Legend of the chart (Ordered from slowest to fastest):

Factorial Complexity — O(n!)
Exponential Complexity — O(2ⁿ)
Quadratic Complexity — O(n²)
Linearithmic Complexity — O(n log n)
Linear Complexity — O(n)
Logarithmic Complexity — O(log n)
Constant Complexity — O(1)